mathematics and art
Főnév
mathematics and art (tsz. mathematics and arts)
- (informatika) A matematika és a művészet két látszólag külön világ, amelyek azonban évszázadok óta kölcsönösen inspirálják egymást. Számos művész és gondolkodó fedezte fel, hogy a geometria és a számok nem csak merev elméleti modellek, hanem látványos esztétikai formákban és arányokban ölthetnek testet. Még a zenében és a táncban is felismerhetők matematikai minták: a zenei hangok és ritmusok arányai, valamint a koreográfiákban előforduló ismétlődések a számok világa felé mutatnak. A képzőművészetben és építészetben különösen sokoldalúan érvényesül a matematika. Itt nem csupán technikai eszközként jelenik meg (például a perspektíva szabályainak alkalmazásában), hanem önálló szerkesztőelveket is szolgáltat (szimmetria, arány, fraktálstruktúrák). A művészek a matematikát gyakran érzelmek és esztétikai élmények kifejezésére használják: Kandinsky például úgy vélte, hogy a geometriai formák és élénk színek egysége mélyebb érzelmi hatást kelt a nézőben. Egyszóval a matematika sehol nem pusztán száraz elmélet; a művészet nyelvén élő és lélegző formákban ölt testet, az emberi érzelmeket is megjelenítve.
Matematikai fogalmak a művészetben
A művészeti alkotásokat irányító matematikai fogalmak közül kiemelt szerepet játszanak az arányok és geometriai szerkezetek. Az aranymetszés (phi ≈ 1,618) például már az ókorban ismert volt, Euklidész említi az arany arányát a geometria szabályai között. Bár később reneszánsz mesterek (Luca Pacioli, Leonardo, Dürer) is foglalkoztak az aranymetszéssel, a legtöbb történészt ma már meggyőzi, hogy az aranymetszés minden műalkotásba véletlenszerű egyezés miatt bukkant fel, nem tudatos tervezés eredményeként. Egy másik, hasonló elgondolású arányt a “plasztikus szám” (kb.1,325) köré csoportosított a holland Hans van der Laan a 20. században. Ez a plastikus arány jellemző 3/4 és 1/7 arányokat eredményez, és ezekkel az értékekkel tervezett templomot Hollandiában.
A reneszánszban vált általános eljárássá a lineáris perspektíva alkalmazása a festészetben. Brunelleschi 15. századi kísérletei meghatározták a távlat szerkesztésének szabályait, a képpont behatárolását fix pontokkal (vanishing point). Brook Taylor és Lambert munkássága pedig a vetületi geometria alapelveit alkotta meg, amire később a festők és építészek rendszeresen építettek. A perspektíva révén a művészetben a tér mélysége és a valósághű távolságok érzete jelenik meg, vagyis maga a geometria teszi lehetővé a látvány hű leképezését.
A szimmetria és ismétlődés is alapvető matematikai gondolat. A múzeumok és templomok díszítéseiben, szőnyegeken, mozaikokon mindig megtalálhatók a tükör- vagy forgásszimmetriák, repülő minták. M. C. Escher grafikái híresek az ilyen mintázatok miatt: végtelenített, ismétlődő parkettázásokkal és látszólag fizikai lehetetlenségekkel (pl. vízesés, spirálok) játszik, miközben a matematikai szabályosságot szemlélteti. A síkban megismétlődő mintázatokra példaként szolgálnak az iszlám geometrikus csempedíszítések (girih-, zellij-mozaikok) vagy a kelta csomóminták – bár ezek sokszor intuitív hagyományból erednek, később a matematikai csoportelmélet eszközeivel elemezhetők (tintacsoportok, tapétacsoportok szerint).
Az 1970-es évektől a számítógépes és algoritmikus művészet is előtérbe került. Itt a művész szoftvert és algoritmusokat használ: felírja a kívánt geometriai szabályt, majd a program generálja a formát. Egy példa erre a Structure Synth szoftverrel készült grafikagyűjtemény, amely spirálokat, csavarvonalakat és poligonokat kombinálva alkot látványos absztrakt képeket. Számítógépes algoritmusokkal ma már fraktálokat és egyéb önhasonló alakzatokat is generálnak, amelyek komplex ismétlődő mintázatokat eredményeznek. A fraktálok (Mandelbrot-halmaz, Julia-halmaz stb.) ismétlődő mintázatai a digitális művészet kedvelt témái: megjelenésükben a végtelen részletgazdagság és önismétlő struktúra fog megfogni a nézőt.
Művészeti formák és anyagok
A matematikai szemlélet különféle művészeti formákban ölthet testet. Az algoritmikus művészet címszó alatt olyan alkotásokat értünk, amelyeket számítógépes kóddal generálnak – ebbe a kategóriába tartozik például a generatív zene vagy a digitális grafika, ahol a hangjegyeket, színeket is szabályrendszer szerint állítják elő. A anamorfikus festészetben a kép csak bizonyos szögből (vagy tükör által) válik azzá, ami – itt a geometriai torzulásokat alkalmazzák látványos trükkökhöz. A modern szobrászati technikák is feltárnak új formákat: az 4D művészet kifejezés olyan installációkat jelölhet, amelyek időben, mozgásban is formálódnak, matematikai modelleket követve (pl. folyadékszimulációk, mozgó fraktálok).
Hagyományosabb közegben is megjelentek matematikai inspirációk. Az origami – a papírhajtogatás – ma már komoly tudományterület: ott geometriai algoritmusokat használnak bonyolult figurák összeállításához, sőt Origami-matematikát is tanítanak. A textilművészetben a csempe- és csipkeminták is szigorúan ismétlődő, gyakran szimmetrikus geometriai struktúrákat mutatnak (például a patchwork-táblák, quilt-minták kitöltése papírra vágott csempealakzatokkal történik). A fonalakból álló string art (fonalrajz) is kifejezetten matematikai: fémszegecseken kifeszített fonalak egyenes vonalakkal görbéket rajzolnak – például gúlákat, paraboloidokat.
Az építészetben is találkozunk különleges formákkal. A piramisformák az ókor óta jelen vannak: a gízai nagy piramis sánchága és alapja közti arány például mindössze 1%-ot tér el az aranymetszéstől. Ugyanakkor a szakmai vélemények szerint ezt feltehetően nem a tervezés idején ismert aranymetszéssel, inkább egyszerű mértani arányokkal alkották meg. A modern építészetben Gaudí épületei példaértékűek: a barcelonai Sagrada Família sétakapujaiban és oszlopaiban olyan térgeometriai felületek szerepelnek, mint a hiperbolikus paraboloidok, catenoidok és láncgörbe-boltívek. Ezek egymásba illeszkedő ívek és lemezek rendkívül erős, mégis könnyű szerkezetet adnak. Buckminster Fuller pedig kidolgozta a geodézikus kupolákat: ezek háromszöghálós kúpszerű burkok, amelyek kiváló teherbíró képességű, szinte azonos sugárú ívekből állnak. A sydney-i Operaház fedelének például egyenlő sugarú gömbrészekből álló csegelyei vannak, így minden irányban azonosan görbült hatású. Ugyancsak érdekes példa a minimális felületű szerkezet: a denveri repülőtér teteje vékony fóliahálóra erősített ún. minimális felületet képez, amely geometriai értelemben legkisebb energiájú burkot ad.
A hagyományos iszlám építészet matematikai gondolkodását a periodikus csempézés (tesszelláció) is jellemzi: mecsetek és paloták falain gyakran találunk kitöltött, ismétlődő geometrikus mintázatokat, amelyek hátterében a síkszimmetriákat osztályozó matematikai elmélet húzódik. Távoli kultúrákban – például a dél-ázsiai Vastu Shastra hagyományában – a templomok alaprajzai és díszítései mandala-alapú, szimmetrikus rendben készülnek, szigorú iránymegszorításokat és arányszámításokat alkalmazva. Összességében az épületek és a művészeti installációk terén a szimmetria, az arányosság és a geometriai mintázatok mind hozzájárulnak egy tárgy vizuális rendjéhez és szépségéhez.
Kiemelkedő művészek és műalkotások
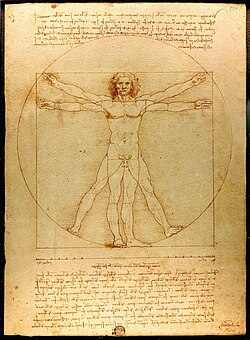
A matematika iránti érdeklődés számtalan nagy művészt inspirált. Az ókorban Polükleitosz a görög szobrászok között kidolgozta az emberi test ideális arányainak Kánonját, míg Vitruvius római építész és író De Architectura című munkájában (ie. 1. század) az épületek harmóniáját az emberi méretekből eredeztette. A reneszánsz korban olyan művészek emelkedtek ki, mint Piero della Francesca, aki De Prospectiva Pingendi című traktátusában leírta a perspektíva szabályait, és aki maga is festményeken alkalmazta az arányokat. Leonardo da Vinci híres „Vitruvius-ember” rajzával a test arányait tette láthatóvá a firenzei Santa Maria Novella festett freskótraktátusa alapján. Albrecht Dürer pedig Vier Bücher von Menschlicher Proportion című írásában az emberi test és perspektíva szabályait foglalta össze. Ők mind a matematikai arányok nyelvén beszéltek a képzőművészetben.
A 19–20. század fordulóján a Platón–Pitagorasz hagyomány újraéledt: William Blake A Teremtő szerepében (The Ancient of Days) kompaszszal rajzolt formát ábrázol az üdvösség kapujában, kifejezve azt a hitet, hogy „Isten folyamatosan geometrizál”. Mellette Johannes Kepler a bolygórendszert alkotta szakrális szabályos testekkel, látomásaival inspirálva a képzőművészetet. Az optikai illúziók és terek paradoxonai Escher grafikáit tették világhírűvé: körforgó lépcsői, vízesése és reptiliái szigorú, végtelenségig ismétlődő mintákat mutatnak, miközben a nézőt meglepik a kép látszólagos lehetetlenségei. Kandinsky az absztrakt festészet úttörőjeként a színekkel és geometriai elemekkel játszott, amelyek elmélyült esztétikai-érzelmi hatást keltenek a nézőben. René Magritte híres képein – például a „La condition humaine”-ben – a valóság végtelen reflexiójára utal, míg Salvador Dalí festményei (Utolsó vacsora, Hiperkocka-keresztre feszítés) egyértelműen utalnak matematikai és geometriai fogalmakra. Dalí 1955-ös Utolsó vacsora című képén például Krisztus és apostolai egy hatoldalú dodekaéder belsejében jelennek meg, jelezve a geometria metafizikai szerepét.
A kortárs művészek közül sokan a digitális korban alkotnak a matematika segítségével. Bathsheba Grossman lézervágott fémszobrokban testesít meg matematikai felületeket, Jan Dibbets és Tony Robbin geometriai installációkat hoz létre, Hamid Naderi Yeganeh algoritmikus rajzai modern fraktálokra emlékeztetnek, István Orosz és Hinke Osinga táblaképeken kísérleteznek anamorfiával. Daina Taimiņa (lett horgolóművész) révén pedig a hiperbolikus geometria is eljutott a közönséghez: valódi csipkefonalból horgolt táblái vizuálisan mutatják meg a nem-euklideszi sík formáit. Összességében a XX–XXI. század művészei a matematika széles spektrumát alkalmazzák: az elvont geometriai eszméktől a konkrét számítógépes algoritmusokig mindent felhasználnak, hogy innovatív, vizuálisan lenyűgöző munkákat hozzanak létre.
Elméleti háttér és szakirodalom
A matematikai módszerek és arányok művészi alkalmazását már az ókortól kezdve különböző írások ismertetik. Polükleitosz „Kánon” című művében leírta az emberi test ideális arányait szobrokhoz. Vitruvius „A tizedik könyv az építészetről” (De Architectura) című munkájában pedig az építészet alapelveit köti az emberi mértékekhez és a geometria szabályaihoz. A reneszánsz elméleti munkák közül Alberti De pictura-ja és De re aedificatoria-ja, Piero della Francesca De prospectiva pingendi-je, Luca Pacioli De divina proportione-ja, valamint Leonardo da Vinci és Dürer aránykönyvei a legismertebbek. Ezek az írások matematikai törvényszerűségeket közvetítettek a művészek felé, például azt, hogyan lehet megrajzolni a valósághoz hű perspektívát vagy hogyan kombinálhatók az arányok a kompozícióban. A 18–19. században megjelentek romantikus és modern művészettörténeti munkák (pl. Jay Hambidge, Owen Jones) és matematikusok szépirodalmi művei is (G. H. Hardy A matematikus gyónása, Hofstadter Gödel, Escher, Bach stb.), amelyek a matematika szépségét vagy esztétikáját vizsgálják.
A szakterületre szakosodott publikációk is működnek. A Journal of Mathematics and the Arts című folyóirat rendszeresen közöl cikkeket a matematikai művészet kapcsolatáról. Létezik a Lumen Naturae nevű újság, valamint olyan konferencia-kiadványok és tanulmánykötetek, amelyek a művészetben felbukkanó perspektíva- és fraktálgeometriával foglalkoznak. Ezekből a forrásokból a hazai érdeklődő is sok ismerethez juthat a téma tudományos és művészi oldaláról.
Társaságok és konferenciák
A tudomány és művészet közötti párbeszédet élénk nemzetközi szervezetek és események tartják fenn. Az egyik legismertebb ilyen a Bridges Organization, amely évente konferenciát rendez matematikai művészet, zene és építészet témában. A Bridges-konferenciákon előadások, kiállítások és műhelyek révén mutatkozik be a legújabb kutatás és kreatív alkotás; az eseményen rendszeresen több tucat ország kutatói és művészei vesznek részt. Hasonló kezdeményezés az európai társaság, a European Society for Mathematics and the Arts, valamint az Ars Mathematica nevű párizsi egyesület. Az Ars Mathematica 1992 óta működik a művészet, tudomány és technológia metszéspontjában, különösen a digitális szobrászat terén tartva biennálé kiállításokat. Emellett számos múzeum és központ foglalkozik matematikai tematikájú múzeumpedagógiával (például a New York-i National Museum of Mathematics – MoMath), illetve műhelyek (Institute For Figuring) népszerűsítik a geometrikus kézművességet és a tudomány esztétikáját. Ezek a szervezetek biztosítanak felületet a kutatók és művészek közötti tapasztalatcserére, valamint a nagyközönség ismerkedésére a matematika művészi vonatkozásaival.
Kapcsolódó témák
Szélesebb értelemben a szent geometria elgondolása is ide kapcsolódik: ez azt vallja, hogy a természet mintázataiban (pl. virágszirmok Fibonacci-számsor szerint, csigaházak spirális arányai stb.) is felismerhetők az univerzum matematikai arányai. A Droste-hatás, amikor egy kép önmagát ismétli (például egy képen belül ugyanazt a képet látjuk kisebb méretben), szintén a végtelen ismétlődés esztétikai játékát hozza a köztudatba. Ugyanakkor a modern tudomány és művészet találkozásában is gyakori a fraktálmintázatok és geometriai algoritmusok vizsgálata, így a matematika művészi kifejezésmódjai a természet mintázatait is visszatükrözhetik.
Összefoglalva, a matematika és a művészet kapcsolata gazdag és sokrétegű. A számok és formák világa és a képzeletbeli alkotás világa kölcsönösen táplálja egymást: a matematikai elvek lehetőséget adnak a kompozíció szerkezetének megtervezésére, a művészi kifejezés pedig érzékelteti ezen elvek szépségét. A szimmetria, arány és perspektíva művészi felhasználása új látásmódot teremt, és alátámasztja, hogy a matematika nem önmagában zárt tudomány, hanem inspirációként szolgálhat a képzőművészet sokféle ágában.
-
Camera lucida in use. Scientific American, 1879
-
Illustration of an artist using a camera obscura. 17th century
-
Proportion: Leonardo's Vitruvian Man, c. 1490
-
Brunelleschi's theory of perspective: Masaccio's Trinità, c. 1426–1428, in the Basilica of Santa Maria Novella
-
Diagram from Leon Battista Alberti's 1435 Della Pittura, with pillars in perspective on a grid
-
Parmigianino, Self-portrait in a Convex Mirror, c. 1523–1524
-
Pythagoras with tablet of ratios, in Raphael's The School of Athens, 1509
-
Oblique projection: Entrance and yard of a yamen. Detail of scroll about Suzhou by Xu Yang, ordered by the Qianlong Emperor. 18th century
-
Oblique projection: women playing Shogi, Go and Ban-sugoroku board games. Painting by Torii Kiyonaga, Japan, c. 1780
-
Base:hypotenuse(b:a) ratios for the Pyramid of Khufu could be: 1:φ (Kepler triangle), 3:5 (3-4-5 Triangle), or 1:4/π
-
Supposed ratios: Notre-Dame of Laon
-
Golden rectangles superimposed on the Mona Lisa
-
Hotamis kilim (detail), central Anatolia, early 19th century
-
Detail of a Ming Dynasty brocade, using a chamfered hexagonal lattice pattern
-
Symmetries: Florentine Bargello pattern tapestry work
-
Ceiling of the Sheikh Lotfollah Mosque, Isfahan, 1619
-
Girih tiles: patterns at large and small scales on a spandrel from the Darb-i Imam shrine, Isfahan, 1453
-
The complex geometry and tilings of the muqarnas vaulting in the Sheikh Lotfollah Mosque, Isfahan
-
Architect's plan of a muqarnas quarter vault. Topkapı Scroll
-
The first printed illustration of a rhombicuboctahedron, by Leonardo da Vinci, published in De Divina Proportione, 1509
-
Mathematical sculpture by Bathsheba Grossman, 2007
-
Fractal sculpture: 3D Fraktal 03/H/dd by Hartmut Skerbisch, 2003
-
Fibonacci word: detail of artwork by Samuel Monnier, 2009
-
Computer art image produced by Desmond Paul Henry's "Drawing Machine 1", exhibited 1962
-
A Bird in Flight, by Hamid Naderi Yeganeh, 2016, constructed with a family of mathematical curves.
-
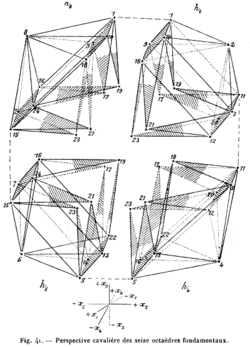
Four-dimensional space to Cubism: Esprit Jouffret's 1903 Traité élémentaire de géométrie à quatre dimensions. Maurice Princet gave a copy to Pablo Picasso, whose sketchbooks for Les Demoiselles d'Avignon illustrate Jouffret's influence.<ref name="Miller">
-
De Stijl: Theo van Doesburg's geometric Composition I (Still Life), 1916
-
A Möbius strip scarf in crochet, 2007
-
Anamorphism: The Ambassadors by Hans Holbein the Younger, 1533, with severely distorted skull in foreground
-
Crocheted coral reef: many animals modelled as hyperbolic planes with varying parameters by Margaret and Christine Wertheim. Föhr Reef, Tübingen, 2013
-
Stimulus to projective geometry: Alberti's diagram showing a circle seen in perspective as an ellipse. Della Pittura, 1435–1436
-
God the geometer. Codex Vindobonensis, c. 1220
-
The creation, with the Pantocrator bearing. Bible of St Louis, c. 1220–1240
-
Johannes Kepler's Platonic solid model of planetary spacing in the Solar System from Mysterium Cosmographicum, 1596
-
William Blake's The Ancient of Days, 1794
-
William Blake's Newton, c. 1800
- mathematics and art - Szótár.net (en-hu)
- mathematics and art - Sztaki (en-hu)
- mathematics and art - Merriam–Webster
- mathematics and art - Cambridge
- mathematics and art - WordNet
- mathematics and art - Яндекс (en-ru)
- mathematics and art - Google (en-hu)
- mathematics and art - Wikidata
- mathematics and art - Wikipédia (angol)